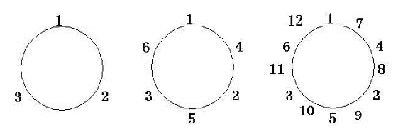21805_JosephusAgain

Traditional Joseph problem is n personal circle, from the first one to start to call the number. The number of people m back from the circle out until only left one person so far.

But now, we think about another Josephus problem. At the first, the circle includes n person. From the first one to start to call the number until call the m, we add a person beside the person who calls the number m, and the new person calls the number at the next round. Repeat this process, until k person in the circle. Now, label the n individuals, for the order of 1 ... n. The new added person label n+1 ... n+k by order. And we are interest in what the label the person whose rank is p.

To simplify the problem, we only think about when m=1. For example, N=3 and k=12, the circle is changed as follows:

Now ,the first one's label is 1 and the second is 7, is third is 4, the forth is 8, the fifth is 2, the sixth is 9, the seventh is 5, the eighth is 10, the ninth is 3, the tenth is 11,the eleventh is 6, the twelfth is 12.

There many cases.

For every case:

The first line, two integer n ( 1≤ n ≤ 10⁹ ), k ( n < k ≤ 10⁹ ), q ( 1 ≤ q <10⁴ ), n is the initial person, k is the final number of person, q is the number of query.

Then next q lines, every line contains an integer p as a query. ( 1 ≤ p ≤ k )

For every case:

Total q lines, for every line, output the person's lable who is now ranked p-th.

3 12 2
3
5

4
2

Hint:

m is always 1.