21972_QuadraticResidues

Pro.ID

21972

Title

Quadratic Residues

Title链接

http://10.20.2.8/oj/exercise/problem?problem_id=21972

AC

0

Submit

0

Ratio

-

时间&空间限制

描述

In 1801, Carl Friedrich Gauss (1777-1855) published his "Disquisitiones Arithmeticae", which basically created modern number theory and is still being sold today. One of the many topics treated in his book was the problem of quadratic residues. 
Consider a prime number p and an integer a !≡ 0 (mod p). Then a is called a quadratic residue mod p if there is an integer x such that 
x² ≡ a (mod p), 
and a quadratic non residue otherwise. Lagrange (1752-1833) introduced the following notation, called the "Legendre symbol":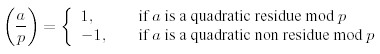 

For the calculation of these symbol there are the following rules, valid only for distinct odd prime numbers p, q and integers a, b not divisible by p: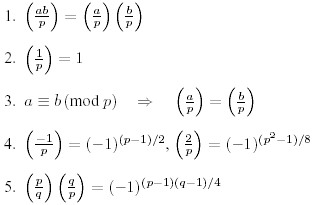 
 
The statements 1. to 3. are obvious from the definition, 4. is called the Completion Theorem, and 5. is the famous Law of Quadratic Reciprocity for which Gauss himself gave no less than six different proofs in the "Disquisitiones Arithmeticae". Knowing these facts, one can calculate all possible Legendre symbols as in the following example: 

输入

输出

Description

In 1801, Carl Friedrich Gauss (1777-1855) published his "Disquisitiones Arithmeticae", which basically created modern number theory and is still being sold today. One of the many topics treated in his book was the problem of quadratic residues. 
Consider a prime number p and an integer a !≡ 0 (mod p). Then a is called a quadratic residue mod p if there is an integer x such that 
x² ≡ a (mod p), 
and a quadratic non residue otherwise. Lagrange (1752-1833) introduced the following notation, called the "Legendre symbol":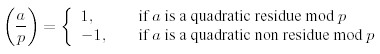 

For the calculation of these symbol there are the following rules, valid only for distinct odd prime numbers p, q and integers a, b not divisible by p: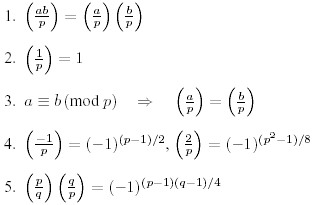 
 
The statements 1. to 3. are obvious from the definition, 4. is called the Completion Theorem, and 5. is the famous Law of Quadratic Reciprocity for which Gauss himself gave no less than six different proofs in the "Disquisitiones Arithmeticae". Knowing these facts, one can calculate all possible Legendre symbols as in the following example: 

Input

The first line contains the number of scenarios. 
For each scenario, there is one line containing the integers a and p separated by a single blank, where 2 < p < 10⁹ is an odd prime, and a satisfies both a !≡ 0 (mod p) and |a| <= 10⁹.

Output

Start the output for every scenario with a line containing "Scenario #i:", where i is the number of the scenario starting at 1. Then print a single line containing (a/p), followed by a blank line.

Sample Input

3
29 79
2 29
1 3

Sample Output

Scenario #1:
-1

Scenario #2:
-1

Scenario #3:
1

Source

TUD 2003

样例输入

3
29 79
2 29
1 3

样例输出

Scenario #1:
-1

Scenario #2:
-1

Scenario #3:
1

提示

作者