Pro.ID10183 TitleJob Processing Title链接http://10.20.2.8/oj/exercise/problem?problem_id=10183 AC4 Submit5 Ratio80.00% 时间&空间限制描述A factory is running a production line that requires two operations to be performed on each job: first operation "A" then operation "B". Only a certain number of machines are capable of performing each operation. 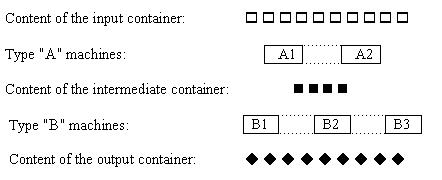 Figure 1 shows the organization of the production line that works as follows. A type "A" machine takes a job from the input container, performs operation "A" and puts the job into the intermediate container. A type "B" machine takes a job from the intermediate container, performs operation "B" and puts the job into the output container. All machines can work in parallel and independently of each other, and the size of each container is unlimited. The machines have different performance characteristics, a given machine requires a given processing time for its operation. Give the earliest time operation "A" can be completed for all N jobs provided that the jobs are available at time 0. Compute the minimal amount of time that is necessary to perform both operations (successively, of course) on all N jobs. 输入Multiple test cases. For each case: Line 1: Three space-separated integers:
Line 2..etc: M1 integers that are the job processing times of each type "A" machine (1..20) followed by M2 integers, the job processing times of each type "B" machine (1..20). 输出Description A factory is running a production line that requires two operations to be performed on each job: first operation "A" then operation "B". Only a certain number of machines are capable of performing each operation.  Figure 1 shows the organization of the production line that works as follows. A type "A" machine takes a job from the input container, performs operation "A" and puts the job into the intermediate container. A type "B" machine takes a job from the intermediate container, performs operation "B" and puts the job into the output container. All machines can work in parallel and independently of each other, and the size of each container is unlimited. The machines have different performance characteristics, a given machine requires a given processing time for its operation. Give the earliest time operation "A" can be completed for all N jobs provided that the jobs are available at time 0. Compute the minimal amount of time that is necessary to perform both operations (successively, of course) on all N jobs. Input Multiple test cases. For each case: Line 1: Three space-separated integers:
Line 2..etc: M1 integers that are the job processing times of each type "A" machine (1..20) followed by M2 integers, the job processing times of each type "B" machine (1..20). Output For each case, output a single line containing two integers: the minimum time to perform all "A" tasks and the minimum time to perform all "B" tasks (which require "A" tasks, of course). Sample Input 5 2 3 Sample Output 3 5 Source 样例输入5 2 3 样例输出3 5 作者 |