Pro.ID22191 TitlePolygon Revolution Title链接http://10.20.2.8/oj/exercise/problem?problem_id=22191 AC0 Submit0 Ratio- 时间&空间限制描述Given a convex polygon with N vertices p[1], ..., p[N] and a line L on a 2-Dimensional plane. You can generate a 3-Dimensional solid of revolution by the revolution of the convex polygon around the axis L. Now your mission is to calculate the volume of this solid.
When the axis L is an external line of the convex polygon, it’s much easier, because the following theorem will help you. But now, be careful, the axis may intersect the convex polygon. The second theorem of Pappus: The volume V of a solid of revolution generated by the revolution of a lamina about an external axis is equal to the product of the area A of the lamina and the distance traveled by the lamina's geometric centroid
 .
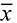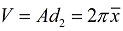
Figure 1 输入The first line of the input is a positive integer T, denoting the number of test cases followed. The first line of each test case is a positive integer N ( 2 < N <= 100 ), which represents the number of vertices of the convex polygon. After that, N lines follow. The i-th ( 1 <= i <= N ) line contains two real numbers Xi ( 0 <= Xi <= 10000 ), yi ( 0 <= yi <= 10000 ) which give the coordinate of the vertices of the convex polygon in clockwise order. Finally, there are three real numbers A, B, C ( -1000 <= A, B, C <= 1000 ) representing the equation of the axis Ax + By + C = 0. 输出Description Given a convex polygon with N vertices p[1], ..., p[N] and a line L on a 2-Dimensional plane. You can generate a 3-Dimensional solid of revolution by the revolution of the convex polygon around the axis L. Now your mission is to calculate the volume of this solid.
When the axis L is an external line of the convex polygon, it’s much easier, because the following theorem will help you. But now, be careful, the axis may intersect the convex polygon. The second theorem of Pappus: The volume V of a solid of revolution generated by the revolution of a lamina about an external axis is equal to the product of the area A of the lamina and the distance traveled by the lamina's geometric centroid
.
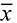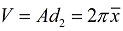
Figure 1 Input The first line of the input is a positive integer T, denoting the number of test cases followed. The first line of each test case is a positive integer N ( 2 < N <= 100 ), which represents the number of vertices of the convex polygon. After that, N lines follow. The i-th ( 1 <= i <= N ) line contains two real numbers Xi ( 0 <= Xi <= 10000 ), yi ( 0 <= yi <= 10000 ) which give the coordinate of the vertices of the convex polygon in clockwise order. Finally, there are three real numbers A, B, C ( -1000 <= A, B, C <= 1000 ) representing the equation of the axis Ax + By + C = 0. Output The output should consist of T lines, one line for each test case, only containing one real number which represents the volume V of the solid of revolution, exact to one decimal after the decimal point. No redundant spaces are needed. Sample Input 2
4
0 0
O 1
1 1
1 0
1 0 0
4
0 0
0 1
1 1
1 0
2 0 -1 Sample Output 3.1
0.8 Source 样例输入2
4
0 0
O 1
1 1
1 0
1 0 0
4
0 0
0 1
1 1
1 0
2 0 -1 样例输出3.1
0.8 作者 |
|Archiver|手机版|小黑屋|同和创作矩阵
( 粤ICP备20019636号-1 )
GMT+8, 2025-2-4 16:06 , Processed in 0.036927 second(s), 14 queries .
Powered by Discuz! X3.4 Licensed
© 2001-2017 Comsenz Inc.
