Pro.ID22793 TitleTo score or not to score Title链接http://10.20.2.8/oj/exercise/problem?problem_id=22793 AC0 Submit0 Ratio- 时间&空间限制描述Robot soccer matches in the very early days were quite funny, since most of the time there wasn't any action in the game. Robots only moved to catch a ball that a robot from the other team had shot. The reason for this somewhat strange behavior was attributed to the used strategy. The robots made a map of all players from the same team and the opponents. If one player was in possession of the ball before even shooting he tried to check whether it was possible to score from the current situation. In the process he checked if there was a way for the ball to reach the goal via several other players of his team. It was possible to shoot the ball to another player if no opponent was close enough to the shooting line to catch the ball. The opponent always moved perpendicular to the shooting line and only if he was sure that he could intercept the shot. The ball always traveled three times as fast as a robot could move, i.e. the player had to be quite near the shooting line to intercept the shot. The other part of the game was fouling another player in order to prevent the other team from reaching the goal. The rules stated that only one player could be fouled at a time, so this only happened if fouling this one player prevented the other team from scoring. Also the initial shooter may not be fouled at anytime. Fouling happens almost instantly by knocking the robot out with an electromagnetic pulse, thus the distance between the two opponents does not matter and the fouling robot does not move. 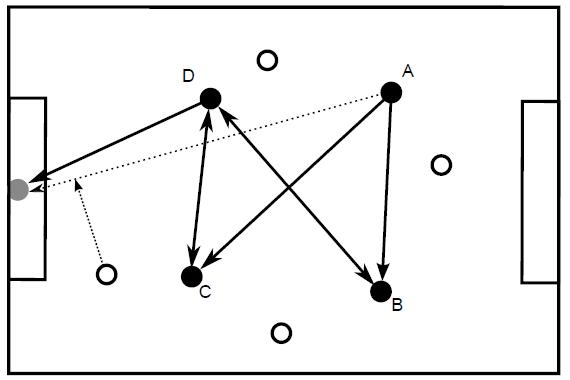 Let's have a look at the figure. There are four players in each team, indicated by the black and white circles. Suppose player A has the ball. Then only the shown shots are possible (note the directions). In all other cases a white player is near enough to intercept the shot (e.g. the direct shot from A to the goal). Thus in principle the black team could score. However, if player D is fouled the goal can no longer be scored. Your university has decided to program a simulator for these ancient robot football matches and your task is to write the part that checks if the team in possession of the ball is able to score or not, based on the current positions of all robots. As a summary of the description above, a team may score if the ball cannot be intercepted by an opponent player and if more than one player would have to be fouled. 输入The first line contains the number of testcases 1 ≤ k ≤ 20 that follow. The first line of each testcase holds the number n of players per team (1 ≤ n ≤ 20). The next 2n lines contain the coordinates of all players, the first n lines being the first team, the second n lines the second team. A coordinate is given as two non-negative floating point numbers separated by spaces. The first player of the first team is in possession of the ball. The coordinates of the goal follow below the two teams. You may assume that the inputs are chosen in such a way that small floating point errors do not lead to wrong results. 输出Description Robot soccer matches in the very early days were quite funny, since most of the time there wasn't any action in the game. Robots only moved to catch a ball that a robot from the other team had shot. The reason for this somewhat strange behavior was attributed to the used strategy. The robots made a map of all players from the same team and the opponents. If one player was in possession of the ball before even shooting he tried to check whether it was possible to score from the current situation. In the process he checked if there was a way for the ball to reach the goal via several other players of his team. It was possible to shoot the ball to another player if no opponent was close enough to the shooting line to catch the ball. The opponent always moved perpendicular to the shooting line and only if he was sure that he could intercept the shot. The ball always traveled three times as fast as a robot could move, i.e. the player had to be quite near the shooting line to intercept the shot. The other part of the game was fouling another player in order to prevent the other team from reaching the goal. The rules stated that only one player could be fouled at a time, so this only happened if fouling this one player prevented the other team from scoring. Also the initial shooter may not be fouled at anytime. Fouling happens almost instantly by knocking the robot out with an electromagnetic pulse, thus the distance between the two opponents does not matter and the fouling robot does not move.  Let's have a look at the figure. There are four players in each team, indicated by the black and white circles. Suppose player A has the ball. Then only the shown shots are possible (note the directions). In all other cases a white player is near enough to intercept the shot (e.g. the direct shot from A to the goal). Thus in principle the black team could score. However, if player D is fouled the goal can no longer be scored. Your university has decided to program a simulator for these ancient robot football matches and your task is to write the part that checks if the team in possession of the ball is able to score or not, based on the current positions of all robots. As a summary of the description above, a team may score if the ball cannot be intercepted by an opponent player and if more than one player would have to be fouled. Input The first line contains the number of testcases 1 ≤ k ≤ 20 that follow. The first line of each testcase holds the number n of players per team (1 ≤ n ≤ 20). The next 2n lines contain the coordinates of all players, the first n lines being the first team, the second n lines the second team. A coordinate is given as two non-negative floating point numbers separated by spaces. The first player of the first team is in possession of the ball. The coordinates of the goal follow below the two teams. You may assume that the inputs are chosen in such a way that small floating point errors do not lead to wrong results. Output Output Goal if the first team is able to score or No goal if the ball can be intercepted or if fouling one player is enough to prevent the team from scoring. Sample Input 2 Sample Output No goal Source 样例输入2 样例输出No goal 作者 |