
一个二叉树的存储方式可以是连续的存储方式(数组)或随机存储方式(链表)。
一、连续存储的二叉树
当使用连续的存储方式时,对于一个完全二叉树来说,子节点编号为2*n,2*n+1,因此仅使用下标即可找到某个节点。但是对于普通二叉树,为了使用数组下标找到节点,需要将其按照完全二叉树补齐,因此需要增加一个值为空的5节点,这样无疑会浪费空间。
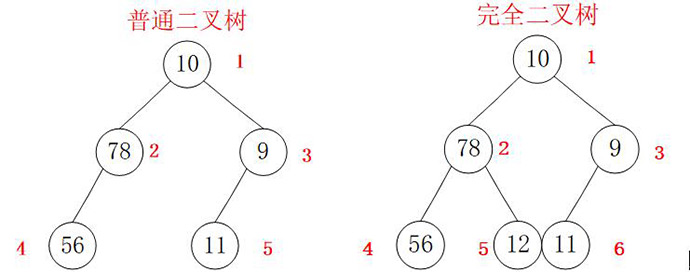
1.声明一个完全二叉树类
本类包含一个数组用来存储二叉树节点。
class BTreeArray<T>
{
private T[] bTree;
private int count;
public BTreeArray(int _number)
{
count = 0;
bTree = new T[_number];
}
public bool Add(T _item)
{
//存储满
if (count >= bTree.Length)
{
ShowInfo("存储空间已满");
return false;
}
//存储数据
bTree[count++] = _item;
return true;
}
private void ShowInfo(string _str)
{
StringBuilder sb = new StringBuilder();
sb.Append("BTree:");
sb.Append(_str);
Console.WriteLine(sb.ToString());
}
}此时可以开辟一段空间并将二叉树的节点存储。
2.实现完全二叉树遍历
a前序遍历(DLR)
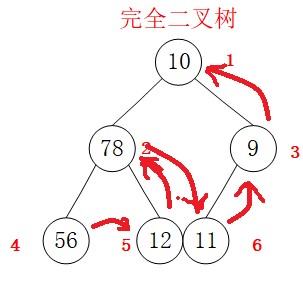
DLR的遍历是先访问根节点,再访问左节点,最后访问右节点。因此遍历的顺序是:
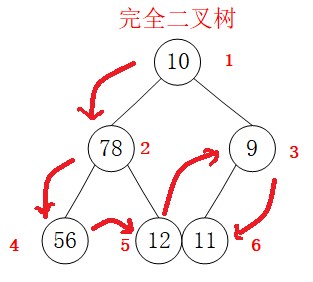
遍历结果应为(10,78,56,12,9,11),编写代码的思路为:分析重复操作:首先访问本节点,然后访问左子节点,最后访问右子节点。在访问左子节点时的操作同样是前述三步操作,因此可以使用递归。代码如下:
private void BTreeDLR(int _index)
{
//节点编号比数组索引大1
int index = _index - 1;
//索引大于总数时,说明节点不存在
if (index >= count)
{
return;
}
//先访问自身
Console.WriteLine(bTree[index]);
//访问左子节点
BTreeDLR(_index * 2);
//访问右子节点
BTreeDLR(_index * 2 + 1);
}
public void BTreeDLR()
{
BTreeDLR(1);
}
测试代码:
int[] data = {10,78,9,56,12,11};
BTreeArray<int> bTree = new BTreeArray<int>(data.Length);
for (int i = 0; i < data.Length; i++)
{
bTree.Add(data[i]);
}
bTree.BTreeDLR();
Console.ReadKey();输出结果:
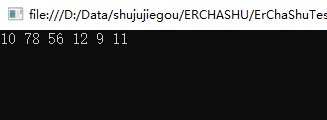
b中序遍历(LDR)
访问顺序如图:
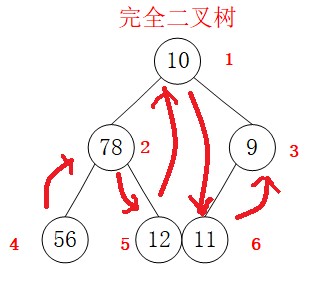
遍历结果为(56,78,12,10,11,9),LDR编写代码的思路为:首先访问左子节点,后访问根节点,最后访问右子节点,重复递归。因此只需在方法中将访问自身、左子节点、右子节点的顺序调换即可,代码如下:
private void BTreeLDR(int _index)
{
//节点编号比数组索引大1
int index = _index - 1;
//索引大于总数时,说明已到该路尽头
if (index >= count)
{
return;
}
//访问左子节点
BTreeLDR(_index * 2);
//访问自身
Console.Write(bTree[index] + " ");
//访问右子节点
BTreeLDR(_index * 2 + 1);
}
public void BTreeLDR()
{
BTreeLDR(1);
}
测试代码:
bTree.BTreeLDR();
运行结果:
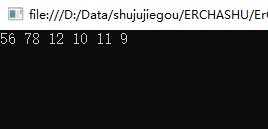
c后序遍历(LRD)
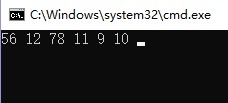
LRD遍历与上同理,编写代码时只需要将访问顺序更换即可。
遍历结果为:56,12,78,11,9,10,代码如下:
private void BTreeLRD(int _index)
{
int index = _index - 1;
if (index >= count)
{
return;
}
BTreeLRD(_index * 2);
BTreeLRD(_index * 2 + 1);
Console.Write(bTree[index] + " ");
}
public void BTreeLRD()
{
BTreeLRD(1);
}测试代码:
bTree.LRD();运行结果:
二、链表存储的二叉树
使用链表存储的好处在于不用考虑欲存储夫人二叉树是否为完全二叉树,同时也不会出现为空的占位节点,得以节省部分内存。但是链表的缺点我们都很熟悉,前一个节点的指针域指向下一个节点,如果前面节点挂了,整条链表GG。在数组中我们寻找某个节点:通过下标表示的内存偏移量直接找到。而在链表中寻找某个节点时,只能由头节点一级一级寻找。
排序二叉树是一种左子节点比根节点小,而右子节点比根节点大的二叉树。这里以一个排序二叉树为例,分别实现删除、添加、修改、遍历。
1.声明排序二叉树
包含一个二叉树节点类,一个二叉树类。
class BTreeLink {
private BTreeLinkNode<int> headNode;
public BTreeLink(BTreeLinkNode<int> _root)
{
headNode = _root;
}
}
class BTreeLinkNode<T> where T:struct
{
public BTreeLinkNode<T> Parent { get; set; }
public BTreeLinkNode<T> LChild { get; set; }
public BTreeLinkNode<T> RChild { get; set; }
public T Data { get; set; }
public BTreeLinkNode(T _data)
{
Data = _data;
}
}2.排序二叉树添加节点
因排序二叉树的结构要求在插入时需要进行排序。
public bool Add(int _data)
{
Console.WriteLine("欲添加" + _data);
BTreeLinkNode<int> node = new BTreeLinkNode<int>(_data);
if (headNode == null)
{
headNode = node;
return true;
}
if (node == null)
{
return false;
}
BTreeLinkNode<int> temp = headNode;
while (true)
{
if (node.Data <= temp.Data)
{
Console.WriteLine("检查,添加值小于"+temp.Data);
//小于,放置在左节点
if (temp.LChild == null)
{
Console.WriteLine("当前节点没有左子节点");
//左节点为空
temp.LChild = node;
node.Parent = temp;
break;
}else
{
temp = temp.LChild;
}
}
else if (node.Data > temp.Data)
{
Console.WriteLine("检查,添加值大于" + temp.Data);
if (temp.RChild == null)
{
Console.WriteLine("当前节点没有右子节点");
//右节点为空
temp.RChild = node;
node.Parent = temp;
break;
}else
{
temp = temp.RChild;
}
}
}
return true;
}运行结果略。
3.排序二叉树寻找节点
public BTreeLinkNode<int> Find(int _data)
{
BTreeLinkNode<int> temp = headNode;
while (true)
{
if (temp == null)
{
//没有找到
return null;
}
if (temp.Data == _data)
{
//找到
return temp;
}
if (_data > temp.Data)
{
//向右寻找
temp = temp.RChild;
}else
{
//向左寻找
temp = temp.LChild;
}
}
}上述寻找操作的死循环还可以使用递归替换。
public BTreeLinkNode<int> Find(int _data,BTreeLinkNode<int> _node)
{
if (_node == null)
{
//跳出
Console.WriteLine("BTree:没有找到值为"+_data+"的节点");
return null;
}
if (_data == _node.Data)
{
return _node;
}
else if (_data < _node.Data)
{
_node = _node.LChild;
}else
{
_node = _node.RChild;
}
//递归
return Find(_data, _node);
}测试代码:
BTreeLinkNode testNode = bTreeLink.Find(19);
BTreeLinkNode testNode1 = bTreeLink.Find(15, root);
if (testNode != null && testNode1 != null)
{
Console.WriteLine("找到了" + testNode.Data);
Console.WriteLine("找到了" + testNode1.Data);
}运行结果:

4.排序二叉树删除节点
由于这是链表存储的排序二叉树,因此删除操作有些麻烦。例如删除节点2,则其下的子节点7和9需要重新连接到二叉树上。思路:将节点2的值修改为左子节点中最大的节点值(14)或右子节点中最小的节点值(16)。
如何找出某节点下的最大节点或最小节点呢?这就是排序二叉树的优势了。最小的节点一定是本节点下最左边的叶子节点,最大的节点一定是本节点下最右边的叶子。由于最小值与最大值在排序二叉树上肯定在叶子节点上,因此赋值完成后将叶子删掉即可。
代码:
public bool Del(int _data)
{
BTreeLinkNode<int> temp = Find(_data);
if (temp == null)
{
Console.WriteLine("BTree::Del:删除失败,不存在值为"+ _data +"的节点");
return false;
}
return Del(temp);
}
public bool Del(BTreeLinkNode<int> _node)
{
BTreeLinkNode<int> temp;
if (_node.LChild == null && _node.RChild == null)
{
//叶子节点,直接删掉
if (_node.Data > _node.Parent.Data)
{
_node.Parent.RChild = null;
}
else
{
_node.Parent.LChild = null;
}
_node.Parent = null;
return true;
}
else if (_node.LChild != null)
{
temp = _node.LChild;
while (temp.RChild != null)
{
temp = temp.RChild;
}
//找到左侧最大值放置于本位置
_node.Data = temp.Data;
Del(temp);
}
else if (_node.RChild != null)
{
temp = _node.RChild;
while (temp.LChild != null)
{
temp = temp.LChild;
}
//找到右侧最小值放置于本位置
_node.Data = temp.Data;
Del(temp);
}
return true;
}测试代码:
bTreeLink.Del(20);
if (bTreeLink.Find(20) == null)
{
Console.WriteLine("20 GG了");
}结果:

5.排序二叉树节点修改
找到该节点把值换了就行,略。
6.排序二叉树前中后序遍历
以DLR前序遍历为例,代码:
private void DLR(BTreeLinkNode<int> _node)
{
if (_node == null)
{
return;
}
Console.Write(_node.Data +" ");
DLR(_node.LChild);
DLR(_node.RChild);
}
public void DLR()
{
DLR(headNode);
}测试代码:
bTreeLink.DLR();运行结果:
总结
连续存储读取速度快,修改方便,但是浪费存储空间,插入删除GG。链表存储读取速度慢,需要从头节点开始向下寻找,且一个节点损坏后面的数据GG,但插入删除方便,更节省存储空间。
引用资料
1、[头图]【HC360】如皋市桃园镇淘淘乐百货经营部 圣诞节新年快乐 墙贴纸批发






